Riprendendo l’argomento trattato il 14 ottobre sulle proprietà dei materiali vorrei approfondire il tema delle superfici perfettamente diffondenti e quindi descriverne le caratteristiche e comportamenti, ne approfitto inoltre per introdurre una relazione molto importante che lega la Luminanza e l’Illuminamento di una superficie lambertiana: la legge del pi.greco o legge di Lambert.
Come già accennato le superfici diffondenti sono superfici teoriche, solo alcune superfici opache si avvicinano per caratteristiche a tali superfici.
Ciò che caratterizza una superficie perfettamente diffondente è la distribuzione delle luminanze indipendente dall’angolo di osservazione, o meglio la luminanza emessa o riflessa è uguale per ogni angolo di osservazione.
Se un raggio di luce incide su una superficie lambertiana questo viene riflesso con un indicatrice di emissione sferica , a palloncino, le intensità luminose emesse sono proporzionali al coseno dell’angolo(θ) compreso tra questa direzione e la normale al piano:

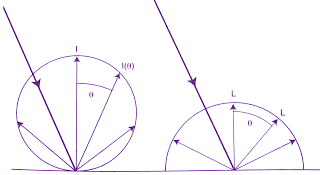
I(θ)=Icosθ dove I=intensità massima perpendicolare al piano: in sostanza si ha una diminuzione graduale dell’intensità man mano che mi avvicino al piano stesso.
Ricordando che la luminanza è data dalla seguente relazione:

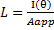
dove Aapp= area apparente in direzione dell’osservatore
Ne segue che

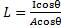
elidendo i coseni ricavo che 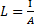(si può vedere anche così I=L*A )
si verifica quanto detto sopra, cioè che la luminanza di una lmbertiana è costante!
Come accennato sopra esiste una relazione che lega la luminanza e l’illuminamento di una superficie perfettamente diffondente: E=πL
Dimostriamo questa relazione:

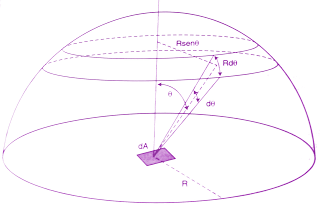
Consideriamo una semisfera e una superficie infinitesima dA posta al centro di essa, dA è caratterizzata da una luminanza costante in ogni direzione L, si consideri infine una anello infinitesimo della semisfera di ampiezza Rd(θ).
L’illuminamento (differenziale) dEr in un punto dell’anello è dato dalla seguente equazione, che deriva dalla I.S.L.:

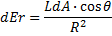
Ricordiamo che E=ϕ/A=flusso/area ne deriva che ϕ=E*A.
Moltiplicando dEr per la superfice dell’anello troveremo la quantità di flusso emesso da dA che incide sull’anello stesso.
Aanello= 2πRsinθ*Rdθ (ovviamente consideriamo l’arco Rdθ come approssimato ad un segmento)
Quindi: dϕr=dEr*2πRsinθ*Rdθ =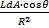*2πRsinθ*Rdθ elido i raggi R n consegue che:
2π*LdA*cosθ*sinθ*dθ. Integrando quest’equazione per la superficie della semisfera ottengo il flusso totale emesso da dA:
dϕtot=2π*LdA*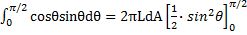

da cui dϕ=πLdA
ne consegue che l’illuminamento in questo caso emettenza è

E=dϕ/dA= πL

Spero sia tutto chiaro, ma soprattutto utile!
Ciao a tutti

Post che ti potrebbero interessare

1. Un po’ di tecnica #2: Illuminamento e Luminanza
2. Legge dell’inverso del quadrato della distanza (ISL)
3. I materiali: riflessione speculare e diffusa
4. Candela e lumen: intensità e flusso luminoso
5. Software per il calcolo illuminotecnico
6. Controllo dell’abbagliamento – UGR (Unified Glare Rating)